1. Float Point 처리 변수 float와 double
세상의 많은 것을 표현하기 위해 우리는 숫자 중에서 실수를 사용 한다. c에서 이것을 표현하기 위해 float와 double가 있다.실제로 프로그램 하다 보다 그렇게 많이 사용되지는 않지만 수학관련 프로그램에서는 당연히 중요한 변수이다. 이 변수에서 숫자의 표현 방식은 국제 표준이 IEEE에 명시된 것으로 컴파일 되는 것이 보통이다. 컴파일러의 설계자가 별도로 다시 정할 필요도 별로 없을 것이다. 자세한 것은 IEEE-754에 규정되어 있다.“ANSI IEEE Standard for Binary Floating-Point Arithmetic”을 참고할 수 있다. 연산은 4칙 연산은 기본적으로
2. CPU 입장에서 본 float와 double
이 변수를 처리하기 위해 CPU에서는 어떻게 처리 할까를 보기 위해서는 CPU의 ALU을 보아야 한다. 현재 나와있는 대부분은 이float point처리를 하지 못한다. 예를 들어 PC에 많이 사용하는 인텔 80X86에서도 CPU내의 모듈에서도 처리 할 수 없다. 이것은 기본적으로 CPU가
l float point을
l 보조 프로세서를 사용한다. 이것을 co-processor(FPU-Floating Point Unit)라고 부른다. 이 코프로세서는 수학연산을 하드웨어 적으로 제공하므로 써 처리 속도를 높인다. 32비트 80386의 메인보드를 보면 별도로 코프로세서를 칩을 장착한 것을 확인할 수 있다. 이 말은 별도의 칩으로 나와있고 이것이 메인보드상에 결합된 것이다. 그래서 인텔에서는 이것을 하나의 칩으로 통합했는데, 이것이 80486 CPU이다. 386과 486(파이프 개념 도입, FPU 한 다이에 통합)의 차이는 CPU의 비트수가 올라간 것이 아니고 32로 유지되어 있음을 알아야 한다. 가끔 486이 64비트가 아닌가 착각하는 경우가 드물게 있다. 586,686 역시 64비트로 알면 안 된다. 그러나 코프로세서가 한 칩 안에 있다고 DSP 칩과 같은 것은 아니다. 이것은 분명 다른 메카니즘으로 작용하고 있다는 것을 알아야 한다. 그래서 80계열의 코프로세서를 사용하기 위해 기계어 코드가 별도로 만들어 졌다. 어셈블러를 보면 FADD,FMUL, ...등 F로 시작하는 기계어 코드는 CPU가 계산하는 것이 아니라 코프로세서로 넘겨 계산 하고 그 결과로 CPU로 가져와 사용한다. 물론
컴파일러를 보면 처리 방식을 함수로 할 것인지 코프로세서로 할 것 인지를 설정할 수 있다. 물론 인텔과 쌍벽을 이루고 있었던 모토롤라의 68계열도 이와 비슷한 변화 과정을 거쳐 발전 해 왔다. 그러면 8비트 계열의 CPU 및 MCU는 대부분 코프로세서가 없는 것이 대부분이다. 따라서 이것은 float을 위한 함수를 제공하는 경우가 있다. 그것은 대부분 32비트인 float만을 제공한다.한번은 32비트의 float을 double로 표시되어 64비트 인 것으로 판단하여 문제가 발생하여 고생한 적이 있어 씁쓸하다. float과double은 국제 표준으로 정해져 있기 때문에 double하면 64비트로 머리 속에 박혀 있던 것이다. 아직도 float로 표시하면 될 것을 왜 굳이 double로 표시 했는지 사기 당한 기분이다. float이라도 있으면 다행인데 이것 마저 없는 컴파일러가 더 많으므로 주의 해야 한다. 64비트 형인 double은 8비트 계열에는 한번도 본적이 없다. 물론 모든 컴파일러를 사용한 것은 아니지만. 이 문제는 계산 결과의 자리수 문제와 연결된다. 다음에 언급하겠지만 32비트 float는 숫자를 나타내는 유효 자리수가 7자리 정도이고 64비트의 double은 16자리 정도 밖에 안됨을 알고 있어야 한다.
float와 double의 표현
표현은 “ANSI IEEE Standard for Binary Floating-Point Arithmetic”에서 표현되어 있어 표준화를 이해 하면 된다.
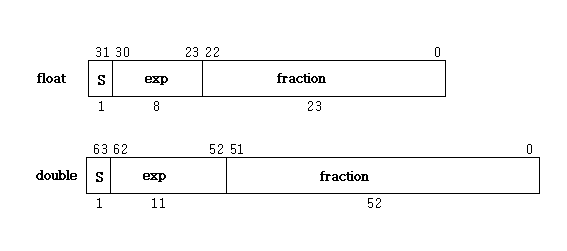
숫자 표현
l 부호 : S 는 +,-로 부호를 나타낸다. 1이면 –이고 0이면 +이다.
l exp : 지수부로 2진수의 지수 이다. 지수부도 부호가 있다.
l fraction : 숫자를 나타낸다. 1보다 작은 숫자를 나타 낸다. 2**(-1) + 2**(-2) + ...
전체적은 다음과 같은 식으로 표현 한다.
(-1) ** S * (1.0 + fraction ) * 2**exp
예를 들어 10진수 1.625는 2진수로는 1.101로 나타낼 수 있다.
이것은
2**0 + [2**(-1) + 2**(-3)]fraction
= 1 + [0.5+0.125]fraction = 1.625
으로 표현할 수 있다.
값변환
http://babbage.cs.qc.edu/IEEE-754/Decimal.html
Type | Minimum value | Maximum value |
float | 1.175494351 E – 38 | 3.402823466 E + 38 |
double | 2.2250738585072014 E – 308 | 1.7976931348623158 E + 308 |
float 표현 (single-precision)
지수부는 8비트에서 +,-을 모두 표현하려면 0x00 ~ 0xFF까지 중에서 부호를 결정하는 방식을 선택해야 한다. 이것은
Exp – 0x7F
를 2의 지수로 한다.
다음과 같은 예를 생각 하면
1.0 : 0 011 1111 1000 0000 0000 0000 0000 0000
지수부에서 “011 1111 1”은 0x7F 이므로
0x7F - 0x7F = 0
이것은 2**0 = 1이다.
이것을 전체 공식에 넣으면
(-1) ** 0 * (1.0 + 0 ) * 1 = 1.0
2번째 예에서
0.75 : 0 011 1111 0100 0000 0000 0000 0000 0000
(-1)**0 * (1.0+2**(-1)) * 2**(0x7E-0x7F)
= 1 * (1.0+0.5) * 2**(-1)
= 1 * (1.5) * 0.5
= 0.75
그러면 실제로 숫자를 표현할 때 한계는 1.18*10**(-38) ~ 3.4*10**38 이다. 그런데 여기서 숫자 중에서 숫자 자릿수는 7자리만이 유효 하다는 한계를 인식하고 있어야 한다. 이것은 간단히 생각하면 fraction 부분이 23자리로 부터 간단히 유도할 수 있다.이것으로 구분하는 것이 숫자의 자릿수이므로 2**23=8,388,608의 가지 수를 구별해 낼 수 있다. 8,388,608의 6자리 만으로 생각할 수 있다. 여기에 1+ fraction와 지수부에서 오는 숫자를 고려하면 대략 7자리 까지는 보장이 된다. 정확한 범위는 수학적으로 계산을 정확히 해야 하지만 여기서는 이 정도의 한계를 집고 넘어간다. 나의 수학적 한계가 여기까지...
따라서 다음과 같은 숫자에서 문제되는 것은
+0.235032543535 * 10**23
2350325는 유효하지만 43535은 나타낼 수 없게 된다. 만약 다음과 같이 print 한다면
float fnum;
fnum = 0.235032543535E23;
printf(“%1.12f”, fnum);
이와 같은 상황이라면 실제로 fnum의 숫자가 0.23503254E23와 같이 입력한 것과 같은 결과이며 뒤의 숫자 43535는 모두 없어지는 결과가 된다. 물론 출력은 모두 되지만 뒤의 숫자는 임의의 숫자임을 알아야 한다.
#include <stdio.h>
int main(int argc, char* argv[])
{
float fnum;
printf("float fnum = 0.235032543535E23;n");
fnum = 0.235032543535E23;
printf("%1.12en", fnum);
return 0;
}
VisualC++6.0 컴파일 결과 :
-----------Configuration: limitreal - Win32 Debug------------
Compiling...
limitreal.cpp
D:limitreallimitreal.cpp(12) : warning C4305: '=' : truncation from 'const double' to 'float'
Linking...
limitreal.exe - 0 error(s), 1 warning(s)
실행 결과 :
float fnum = 0.235032543535E23;
2.350325513093e+022
1 00000000 00000000000000000000000 = -0
0 11111111 00000000000000000000000 = Infinity
1 11111111 00000000000000000000000 = -Infinity
0 11111111 00000100000000000000000 = NaN
1 11111111 00100010001001010101010 = NaN
0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1.0 = 2
0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1.101 = 6.5
1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1.101 = -6.5
0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1.0 = 2**(-126)
0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0.1 = 2**(-127)
0 00000000 00000000000000000000001 = +1 * 2**(-126) *
0.00000000000000000000001 =
2**(-149) (Smallest positive value)
double 표현 (double-precision)
float가 32비트 이라면 64비트로 확장한 것이 double이다. 계산 방식은 같으나 각 숫자요소가 확장되어 있으므로 이것만 고려하면 된다.
지수부는 11비트 이므로
Exp – 0x3FF
가 2의 지수가 되어 다음과 같이 계산 된다.
0.75 : 0 011 1111 1110 1000 0000 0000 0000 0000 0000 ... 0000
(-1)**0 * (1.0+2**(-1)) * 2**(0x3FE-0x3FF)
= 1 * (1.0+0.5) * 2**(-1)
= 1 * (1.5) * 0.5
= 0.75
숫자의 한계를 알기 위해 다음과 같이 프로그램 하였다.
#include <stdio.h>
int main(int argc, char* argv[])
{
float fnum;
printf("float fnum = 0.235032543535E23;n");
fnum = 0.235032543535E23;
printf("%0.20en", fnum);
printf("float fnum = 0.123456789012345E23;n");
fnum = 0.123456789012345E23;
printf("%0.20en", fnum);
printf("float fnum = 0.123451234512345E10;n");
fnum = 0.123451234512345E10;
printf("%0.20en", fnum);
printf("n");
double dnum;
printf("double dnum = 0.123456789012345E23;n");
dnum = 0.123456789012345E23;
printf("%0.12len", dnum);
printf("double dnum = 0.123456789012345678901234567890E3;n");
dnum = 0.123456789012345678901234567890E3;
printf("%.20len", dnum);
return 0;
}
float fnum = 0.235032543535E23;
2.35032551309319510000e+022
float fnum = 0.123456789012345E23;
1.23456793779139080000e+022
float fnum = 0.123451234512345E10;
1.23451238400000000000e+009
double dnum = 0.123456789012345E23;
1.234567890123e+022
double dnum = 0.123456789012345678901234567890E3;
1.23456789012345680000e+002
| No. | Parameter | Format | |||||
|---|---|---|---|---|---|---|---|
Single | Single Extended | Double | Double Extended | Quadruple?+ | Extended?# | ||
| (1) | p (precision, apparent mantissa width in bits) | 24 | ≥ 32 | 53 | ≥ 64 | 113 | 64 |
| (2) | Decimal digits of precision p / log2(10) | 7.22 | ≥ 9.63 | 15.95 | ≥ 19.26 | 34.01 | 19.26 |
| (3) | Mantissa’s MS-Bit | hidden bit | unspecified | hidden bit | unspecified | hidden bit | explicit bit |
| (4) | Actual mantissa width in bits | 23 | ≥ 31 | 52 | ≥?63 | 112 | 64 |
| (5) | Emax | +127 | ≥ +1023 | +1023 | ≥ +16383 | +16383 | +16383 |
| (6) | Emin | -126 | ≤ -1022 | -1022 | ≤ -16382 | -16382 | -16382 |
| (7) | Exponent bias | +127 | unspecified | +1023 | unspecified | +16383 | +16383 |
| (8) | Exponent width in bits | 8 | ≥ 11 | 11 | ≥ 15 | 15 | 15 |
| (9) | Sign width in bits | 1 | 1 | 1 | 1 | 1 | 1 |
| (10) | Format width in bits (9) + (8) + (4) | 32 | ≥ 43 | 64 | ≥ 79 | 128 | 80 |
| (11) | Range Magnitude Maximum 2Emax?+?1 | 3.4028E+38 | ≥ 1.7976E+308 | 1.7976E+308 | ≥ 1.1897E+4932 | 1.1897E+4932 | 1.1897E+4932 |
| (12) | Range Magnitude Minimum 2Emin | 1.1754E-38 | ≤ 2.2250E-308 | 2.2250E-308 | ≤?3.3621E-4932 | 3.3621E-4932 | 3.3621E-4932 |
| (13) | Range Magnitude Minimum (Denormalized) ??2Emin?-?(4) | 1.4012E-45 | ≤ 1.0361E-317 | 4.9406E-324 | ≤ 3.6451E-4951 | 6.4751E-4966 | 1.8225E-4951 |
| (14) | FORTRAN Language Type | REAL*4 | ? | REAL*8 | ? | REAL*16 | REAL*10 |
| (15) | C Language Type | float | ? | double | ? | long double | long double |
32-bit Single Precision
| Range Name | Sign (s) 1 [31] | Exponent (e) 8 [30-23] | Mantiss a(m) 23 [22-0] | Hexadecimal Range | Range | Decimal Range § |
|---|---|---|---|---|---|---|
| Quiet -NaN | 1 | 11..11 | 11..11 : 10..01 | FFFFFFFF : FFC00001 | ? | ? |
| Indeterminate | 1 | 11..11 | 10..00 | FFC00000 | ? | ? |
| Signaling -NaN | 1 | 11..11 | 01..11 : 00..01 | FFBFFFFF : FF800001 | ? | ? |
| -Infinity (Negative Overflow) | 1 | 11..11 | 00..00 | FF800000 | < -(2-2-23) × 2127 | ≤ -3.4028235677973365E+38 |
| Negative Normalized -1.m × 2(e-127) | 1 | 11..10 : 00..01 | 11..11 : 00..00 | FF7FFFFF : 80800000 | -(2-2-23) × 2127 : -2-126 | -3.4028234663852886E+38 : -1.1754943508222875E-38 |
| Negative Denormalized -0.m × 2(-126) | 1 | 00..00 | 11..11 : 00..01 | 807FFFFF : 80000001 | -(1-2-23) × 2-126 : -2-149 (-(1+2-52) × 2-150)?* | -1.1754942106924411E-38 : -1.4012984643248170E-45 (-7.0064923216240862E-46)?* |
| Negative Underflow | 1 | 00..00 | 00..00 | 80000000 | -2-150 : < -0 | -7.0064923216240861E-46 : < -0 |
| -0 | 1 | 00..00 | 00..00 | 80000000 | -0 | -0 |
| +0 | 0 | 00..00 | 00..00 | 00000000 | 0 | 0 |
| Positive Underflow | 0 | 00..00 | 00..00 | 00000000 | > 0 : 2-150 | > 0 : 7.0064923216240861E-46 |
| Positive Denormalized 0.m × 2(-126) | 0 | 00..00 | 00..01 : 11..11 | 00000001 : 007FFFFF | ((1+2-52) × 2-150)?* 2-149 : (1-2-23) × 2-126 | (7.0064923216240862E-46)?* 1.4012984643248170E-45 : 1.1754942106924411E-38 |
| Positive Normalized 1.m × 2(e-127) | 0 | 00..01 : 11..10 | 00..00 : 11..11 | 00800000 : 7F7FFFFF | 2-126 : (2-2-23) × 2127 | 1.1754943508222875E-38 : 3.4028234663852886E+38 |
| +Infinity (Positive Overflow) | 0 | 11..11 | 00..00 | 7F800000 | > (2-2-23) × 2127 | ≥?3.4028235677973365E+38 |
| Signaling +NaN | 0 | 11..11 | 00..01 : 01..11 | 7F800001 : 7FBFFFFF | ? | ? |
| Quiet +NaN | 0 | 11..11 | 10..00 : 11..11 | 7FC00000 : 7FFFFFFF | ? | ? |
64-bit Double Precision
| Range Name | Sign(s) 1 [63] | Exponent (e) 11 [62-52] | Mantissa (m) 52 [51-0] | Hexadecimal Range | Range | Decimal Range § |
|---|---|---|---|---|---|---|
| Quiet -NaN | 1 | 11..11 | 11..11 : 10..01 | FFFFFFFFFFFFFFFF : FFF8000000000001 | ? | ? |
| Indeterminate | 1 | 11..11 | 10..00 | FFF8000000000000 | ? | ? |
| Signaling -NaN | 1 | 11..11 | 01..11 : 00..01 | FFF7FFFFFFFFFFFF : FFF0000000000001 | ? | ? |
| -Infinity (Negative Overflow) | 1 | 11..11 | 00..00 | FFF0000000000000 | < -(2-2-52) × 21023 | ≤ -1.7976931348623158E+308 |
| Negative Normalized -1.m × 2(e-1023) | 1 | 11..10 : 00..01 | 11..11 : 00..00 | FFEFFFFFFFFFFFFF : 8010000000000000 | -(2-2-52) × 21023 : -2-1022 | -1.7976931348623157E+308 : -2.2250738585072014E-308 |
| Negative Denormalized -0.m × 2(-1022) | 1 | 00..00 | 11..11 : 00..01 | 800FFFFFFFFFFFFF : 8000000000000001 | -(1-2-52) × 2-1022 : -2-1074 (-(1+2-52) × 2-1075)?* | -2.2250738585072010E-308 : -4.9406564584124654E-324 (-2.4703282292062328E-324)?* |
| Negative Underflow | 1 | 00..00 | 00..00 | 8000000000000000 | -2-1075 : < -0 | -2.4703282292062327E-324 : < -0 |
| -0 | 1 | 00..00 | 00..00 | 8000000000000000 | -0 | -0 |
| +0 | 0 | 00..00 | 00..00 | 0000000000000000 | 0 | 0 |
| Positive Underflow | 0 | 00..00 | 00..00 | 0000000000000000 | > 0 : 2-1075 | > 0 : 2.4703282292062327E-324 |
| Positive Denormalized 0.m × 2(-1022) | 0 | 00..00 | 00..01 : 11..11 | 0000000000000001 : 000FFFFFFFFFFFFF | ((1+2-52) × 2-1075)?* 2-1074 : (1-2-52) × 2-1022 | (2.4703282292062328E-324)?* 4.9406564584124654E-324 : 2.2250738585072010E-308 |
| Positive Normalized 1.m × 2(e-1023) | 0 | 00..01 : 11..10 | 00..00 : 11..11 | 0010000000000000 : 7FEFFFFFFFFFFFFF | 2-1022 : (2-2-52) × 21023 | 2.2250738585072014E-308 : 1.7976931348623157E+308 |
| +Infinity (Positive Overflow) | 0 | 11..11 | 00..00 | 7FF0000000000000 | > (2-2-52) × 21023 | ≥ 1.7976931348623158E+308 |
| Signaling +NaN | 0 | 11..11 | 00..01 : 01..11 | 7FF0000000000001 : 7FF7FFFFFFFFFFFF | ? | ? |
| Quiet +NaN | 0 | 11..11 | 10..00 : 11..11 | 7FF8000000000000 : 7FFFFFFFFFFFFFFF | ? | ? |
§ Your least significant digits may differ.
3. 수학계산 함수
컴파일러는 수학 계산을 위해서는 함수를 lib로 지원하는데 일반적인 공학 계산은 할 수 있다.
l 4칙연산
4칙연산은
어떻게 연산되는지를 확인하기 다음과 같은 간단한 프로그램을 생각한다.
float f1;
float f2;
float fares;
float fsres;
float fmres;
float fdres;
void cfloat(void)
{
fares = f1 + f2;
fsres = f1 - f2;
fmres = f1 * f2;
fdres = f1 / f2;
}
PUBLIC _f1 ; f1
PUBLIC _f2 ; f2
PUBLIC _fares ; fares
_BSS SEGMENT ; 초기값 없는 section
global 변수 3개는 float 이므로 32비트 영역의 변수 공간 이다.
_f1 DD 01H DUP (?) ; f1
_f2 DD 01H DUP (?) ; f2
_fares DD 01H DUP (?) ; fares
_BSS ENDS
_TEXT SEGMENT
_cfloat PROC NEAR ; cfloat, COMDAT
다음은 float의 더하기 인데 모두 코프로세서(FPU)로 전이되어 계산한다.
; fares = f1 + f2;
00000 d9 05 00000000 fld DWORD PTR _f2 ; f2-FPU의 oper 레지스터로 f2변수값을 전송한다.
00006 d8 05 00000000 fadd DWORD PTR _f1 ; f1–oper와 f1의 메모리 변수값과 더한다.
0000c d9 1d 00000000 fstp DWORD PTR _fares ; fares–FPU에서 더해진 값을 저장 한다. =의 실행이다.
; fsres = f1 - f2;
00012 d9 05 00 00 00 00 fld DWORD PTR _f1 ; f1
00018 d8 25 00 00 00 00 fsub DWORD PTR _f2 ; f2
0001e d9 1d 00 00 00 00 fstp DWORD PTR _fsres ; fsres
; fmres = f1 * f2;
00024 d9 05 00 00 00 00 fld DWORD PTR _f2 ; f2
0002a d8 0d 00 00 00 00 fmul DWORD PTR _f1 ; f1
00030 d9 1d 00 00 00 00 fstp DWORD PTR _fmres ; fmres
; fdres = f1 / f2;
00036 d9 05 00 00 00 00 fld DWORD PTR _f1 ; f1
0003c d8 35 00 00 00 00 fdiv DWORD PTR _f2 ; f2
00042 d9 1d 00 00 00 00 fstp DWORD PTR _fdres ; fdres
; }
00048 c3 ret 0
_cfloat ENDP ; cfloat
_TEXT ENDS
이번에는 삼각함수의 예이다.
_BSS SEGMENT
_fres DQ 01H DUP (?) ; double fres; - 64비트 공간을 설정 한다.
_BSS ENDS
PUBLIC _ffun ; ffun
PUBLIC _d0.4_3fd999999999999a ; 함수 호출할 때 사용되어질 0.4의 값을 정의한다.
; COMDAT _d0.4_3fd999999999999a
CONST SEGMENT
_d0.4_3fd999999999999a DQ 03fd999999999999ar ; 0.4
CONST ENDS
; COMDAT _ffun
_TEXT SEGMENT
_ffun PROC NEAR ; ffun, COMDAT
; fres = tan(0.4);
00000 dd 05 00 00 00 00 fld QWORD PTR _d0.4_3fd999999999999a
- 정수값 이라면 코드 다음에 숫자가 오지만 64비트의 double은 위와 같이 처리된다.
00006 d9 f2 fptan
00008 dd d8 fstp ST(0)
0000a dd 1d 00 00 00 00 fstp QWORD PTR _fres ; fres
; }
00010 c3 ret 0
_ffun ENDP ; ffun
_TEXT ENDS
삼각함수 역시 함수가 아니라 FPU가 연산 한다.
이에 반해 FPU가 없는 경우를 보기 위해 ARM으로 컴파일 해보면
|x$dataseg|
f1
DCFS 0.0
f2
DCFS 0.0
cfloat
|L000000.J2.cfloat|
STMDB sp!,{v1-v3,lr}
LDR v1,[pc, #L000054-.-8]
LDR a2,[v1,#4]
LDR a1,[v1,#0]
MOV v2,a2
MOV v3,a1
BL _fadd
. . .
LDMIA sp!,{v1-v3,pc}
L000054
DCD |x$dataseg|
와 같이 함수 호출을 함을 알 수 있다. 이 함수를 다음 map 파일에서 확인할 수 있다.
AREA map of D:programARMReleasemath.axf:
Base Size Type RO? Name
8000 4c CODE RO !!! from object file __main.o
804c 164 CODE RO C$$code from object file fcalc.o
81b0 10 CODE RO C$$code from object file main.o
81c0 224 CODE RO C$$code from object file fadd.o
83e4 12c CODE RO C$$code from object file fmul.o
8510 1dc CODE RO C$$code from object file fdiv.o
86ec e0 CODE RO C$$code from object file dadd.o
87cc d4 CODE RO C$$code from object file dmul.o
88a0 144 CODE RO C$$code from object file ddiv.o
89e4 40 CODE RO C$$code from object file sin.o
8a24 58 CODE RO C$$code from object file cos.o
8a7c 18c CODE RO C$$code from object file tan.o
CPU와 코프로세서가 결합되어 있지 않은 경우는 float point을 처리하기 위해 필연적으로 함수를 사용할 수 밖에 없다. 이것은 저속의 CPU에서는 동작 시간 및 리얼타임의 문제를 미리 검토하여 설계하여야 문제가 적어진다.
4. 삼각 함수의 계산
삼각함수를 계산하기 위해서는 각도가 존재 한다. 삼각함수를 계산하는 대부분은 래디언 각도로 인수를 설정해야 한다. 계산기에서는 보통 360도의 숫자로 사용하지만 프로그램 함수는 다르다. 다음 프로그램을 생각해 본다.
#include <stdio.h>
#include <math.h>
#define PI (double)3.1415926535
int main(int argc, char* argv[])
{
double rst;
rst = sin( 45.);
printf("sin(45.) = %lf - 360도 기준이 아님.n", rst);
double ideg;
double deg;
ideg = 45.;
deg = ideg*(PI/180.); // 360도 기준을 2PI로 바꾼다.
printf("sin( %lf ) = %lfn", ideg, sin(deg));
printf("cos( %lf ) = %lfn", ideg, cos(deg));
printf("tan( %lf ) = %lfn", ideg, tan(deg));
return 0;
}
실행 결과 :
sin( 45. ) = 0.850904 - 360도 기준이 아님.
sin( 45.000000 ) = 0.707107
cos( 45.000000 ) = 0.707107
tan( 45.000000 ) = 1.000000
“sin( 45. ) = 0.850904”의 결과는 계산기를 눌러보면 답이 다름을 할 수 있다. 다음 줄의 결과 값이 맞는 것이다. 360도가 아니라 2*PI 기준으로 인수를 넣어야 한다. 이것은 각도에다 PI/180을 곱해야 2PI 기준으로 바꾸어 진 것이다.
5. float point 변수의 array와 포인터
float fdata[100];
float *pfdt;
여기서 array는 기본 규칙에 따르는데, 시작 주소로 부터 차례로 sizeof(float) 만큼 씩 주소가 증가하면서 배치된다.
pfdt = fdata;
와 같이 주소값을 처리 한다.
간단히 합하는 프로그램을 작성하면 다음과 같은
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char* argv[])
{
srand( (unsigned)time( NULL ) ); // 프로그램의 시작 시간이
// 정해져 있지 않기 때문에 rand seed로 사용한다.
float *pfdt;
float sum;
int cnt;
float calcSum(float *pfdt, int length);
pfdt = new float[100];
for (cnt = 0;cnt < 100;cnt++) {
pfdt[cnt] = (float) rand();
}
sum = calcSum(pfdt, 100);
printf("sum=%fn", sum);
delete [] pfdt;
return 0;
}
float calcSum(float *pfdt, int length)
{
float fsum;
fsum = 0.0f;
for (;length;length--) {
fsum += *pfdt++;
}
return fsum;
}
여기서 다음 코드를 생각하면 기본적인 틀에 의해 해석된다.
fsum += *pfdt++;는
다음 2라인으로 표시할 수 있는데
fsum += *pfdt;
pfdt++;
포인터는 다른 타입의 변수 처럼 CPU에 의해 정해진 길이 주소값을 갖는 변수이고
pfdt++는 pfdt <= pfdt의 주소값 + sizeof(float)로 코딩 된다.
